For most of Western history, the name of Euclid has been synonymous with that of geometry, and the science of space. Euclid's shadow is a hard one to surpass, but he is not without his limits. For just as Kant criticized Aristotle for postulating categories without method or guidance, so too Schopenhauer criticized Euclid for proceeding to construct a system with neither blueprint nor solid foundations. The five postulates which begin the Elements are dropped on the table without explanation, without grounding, and then a circuitous assemable of theorems are produced, without any explicit reason as to the method or trajectory of an undergirding theory of geometry.

Bernhard Riemann was one of the first modern minds to grapple with the question of how we can ground geometry as a science of space. In his inaugural lecture, Über die Hypothesen, welche der Geometrie zu Grunde liegen, Riemann attempted to tackle this question through considering the nature of a multiplicity, a multi-dimensional entity in space. His presentation in this lecture is considered foundational to mathematic topology, and was rather influential on Einstein as well. Riemann even gestures in the closing of this lecture to physics as a science that can lead the way forward in understanding the nature of space.

This lecture has two translations that I could find. William Clifford in Nature, vol. 8, pp. 14-17, 36-37. And Michael Spivak, A Comprehensive Introduction to Differential Geometry vol. II, pp. 135-153.

I have attempted a new translation because Spivak's is not readily available without purchase of his book, and Clifford's translation does not use the most up-to-date terminology. Translation is a fruitful exercise, and I hope anyone interested in the foundations of topology will give Riemann's pioneering study some consideration.

---

Overview

Plan of the Investigation

I. Concept of an n-folded extended quantity

§1. Continuous and discrete multiplicities. Certain parts of a of a multiplicity are called quanta. Division of the doctrine of continuous quantities into the doctrine...
    (1) Of mere area relations, where an independence of the quantities from from space is not assumed.
    (2) Of proportions, for which such indpendence must be assumed.
§2. Generation of the concept of a single, double, n times extended multiplicity.
§3. Reduction of a location determination in a given multiplicity to quantity determinations.

II. The proportions by which a multiplicity of n dimensions is measurable by every line, assuming that the lines have a length independent of position

§1. Expression of the linear element. Such multiplicities are considered even where the linear element is given by the square root of a sum of complete differentials.
§2. Investigation of an n-fold extended multiplicity in which the linear element is represented by the square root of a quadratic differential. The measure of its deviation from flatness (curvature) in a given point and a given surface direction. Fot the determination of their proportions it is (under certain restrictions) permissible and sufficient that the curvature be given arbitrarily at every point in (n*(n+1))/2 surface directions.
§3. Geometric illustration.
§4. Flat multiplicities (where curvature = 0 everywhere) may be treated as a special case of multiplicity with constant curvature. These can be defined by the fact that in them the independence of n times extended quantities from position (possibility of motion without stretching).
§5. Surfaces with constant curvature.

III. Application to Space

§1. Systems of facts which are necessary for the determination of proportions, as geometry presupposes them.
§2. How probable and to what extent are these empirical determinations valid beyond the limits of observation toward the infinitely large?
§3. How far towards the infinitesimal? Connection of this question with the interpretation of nature.

The Plan of the Investigation

It is well known that geometry presupposes both the concept of space as the first grounding concept for the constructions in space as something given. It only gives nominal definitions of these, whereas the essential rules are given in the form of axioms. The relation of these presuppositions remains obscure; one does not see if and to what extent their connection is necessary, nor a priori if it is possible.

This obscurity was also not taken into account from Euclid or Legendre (to name the most famous recent reformer of geometry), neither by the the mathematicians, nor by the philosophers who dealt with it. This was likely due to the fact that the general concept of a multiplicity extended quantity (in which spatial quantities are included) remained entirely untreated. I have therefore first set myself the task of defining the concept of a multiplicity extended quantity from general concepts of quantity. It will follow from this that an extended quantity is capable of different proportions and that space is only a special of a threefold extended quantity. But from this, it is a necessary result that the theorems of geometry cannot be derived from general concepts of quantity, but that those properties which distinguish space from other conceivable threefold extended quantity can only be derived from experience. Out of this arises the task to find the simplest facts from which the proportions of space can be determined--a task which by the nature of the matter, is not fully determined; for several systems of simple facts can be given which are sufficient for determining spatial proportions; of which the most important for the present purpose is the one based on Euclid. These facts are, like all facts, not necessary but only of empirical certainty, they are hypotheses; therefore one can investigate their probability, which within the limits of observation however is very large, and thereafter decide upon the extent of their legitimacy beyonds the limits of observation, both on the the side of the infinitely large and infinitely small.

I. Concept of an n-folded extended quantity

While I now undertake to solve the first of these tasks, the development of the concept of multiplicity extended quantities, I believe I am all the more entitled to lenient assessment, because in such works of a more philosophical nature, where the difficulties lie more in the concepts than in the construction, I am little trained, outside a few suggestions, which Mr. Privy Councilor Gauss had given in the second treatise on Biquadratic Remainders, in the Göttingen Gelehrte Anzeige and in his Jubilee book, and some of Herbart's philosophical research, I could make use of no preliminary work whatsoever.

§ 1.

Concepts of quantity are only possible where there is a general concept which permits various determinations. These determinations depend from one to another on whether they form a continuous or discrete multiplicity; in the former case the individual determinations are called points, and in the latter case elements. Concepts whose determinations form a discrete multiplicity, are so frequent, that for any given thing at least in the more sophisticated languages, a concept can always be found under which they are contained (and the mathematicians could therefore, in the doctrine of discrete magnitudes, unhesitatingly assume the requirement that given things are to be regarded as discrete quantities), whereas the causes for the formation of concepts, the determinations of which form a continuous multiplicity, are so rare in ordinary life that the places of sense-objects and the colors are likely the only simple concepts. The more frequent cause for the creation and development of these concepts occurs first in higher mathematics.

Certain parts of a multiplicity, distinguished by an attribute or distinguishing boundary, are called quanta. Their comparison to quantity is done by counting in the case of discrete quantities and by measuring in the case of continuous quantities. Measure consists in a superpositioning of compared quantities; measure therefore requires a means of using quantity as a standard for another. Lacking this, two quantities can only be compared, when one is part of the other, and also then only as more or less, not as "how much". The investigation which can be made about them in this case form a general division of the theory of quantity that is independent of determinations of measure, where the quantities are not thought to exist independently of the position and not expressible in terms of a unit, but rather as areas in a multiplicity. Such investigations are of great importance for several aspects of mathematics, especially for the treatment of the multi-value analytic functions, and the lack of such investigations is probably one of the main reasons that Abel's noteworthy theorem and the achievements of Lagrange, Pfaff, Jacobi for the general theory of differential equations, have for so long remained unfruitful. Out of this general part of the theory of extended quantities, where nothing more is assumed than what is already contained in their concept, it is sufficient to highlight two points for the present purpose: the first of which is concerned with the creation of the concept of a multiply extended multiplicity, the second is the reduction of determinations of place in a given multiplicity to quantitative determinations and to make clear the essential character of an n-fold extension.

§ 2.

If one proceeds with a concept whose determinations form a continuous multiplicity, one passes from one mode of determination in a certain way over into another, so the passed-through modes of determination form a simply extended multiplicity who essential character is that continuous progress from a point is possible only in two aspects: forwards or backwards. If one now imagines that this multiplicity passes again into another, completely different one, and that again in a definite way, i.e. in such a way that every point passes into a certain point of the other multiplicity, then all modes of determination obtained in this way form a twofold extended multiplicity. In a similar way one obtains a threefold extended multiplicity if one imagines that a twofold extended multiplicity merges in a certain way into another multiplicity that is entirely different. And it is easy to see how this construction can carry on. If one, instead of considering the concept determinable, considers its object as variable, this construction can be described as a composition of a variability of n + 1 dimensions out of a variability of n dimensions and a variability of one dimension.

§ 3.

I will now show conversely how to transform a variability whose area is given into a variability of one dimension and a variability of fewer dimensions. To this end consider a variable piece of a multiplicity of one dimension--reckoned from a fixed starting point, so that its values can be compared among one another--which has for every point of the given multiplicity a definite value which continuously varies with it. Or in other words, assume a continuous function of position within the given multiplicity which furthermore is not constant in any part of that multiplicity. Every system of points where the function has a constant value, then forms a continuous multiplicity of fewer dimensions than the given one. These multiplicities continuously merge into each other when the function is changed; therefore, one can assume that from one of them the remaining ones emerge, and this, speaking generally, may occur in such a way that each point merges into a certain point of the others. Exceptions, whose investigation are important, can be left unconsidered. From this, the determination of position in the given multiplicity is reduced to a quantitative determination and a determination of position in a multiplicity of fewer dimensions. It is now easy to show that this multiplicity has n - 1 dimensions, if the given multiplicity is an n-fold extended multiplicity. Therefore, by repeating this process n times, the determination of position in an n-fold extended multiplicity is reduced to n determinations of quantity, and thus the position in a given multiplicity, when this is possible, is reduced to a finite number of determinations of quantity. However there are multiplicities in which the determination of position requires a non-finite number, but rather an infinite series or a continuous multiplicity of quantitative determination. Such multiplicities are for example the possible determinations of a function for a given area, the possible shapes of a spatial figure, etc.

II. The proportions by which a multiplicity of n dimensions is measurable by every line, assuming that the lines have a length independent of position

It follows now, that after the concept of an n-fold extended multiplicity has been constructed and as an essential characteristic of it has been found that the determination of its location can be reduced to n determinations of magnitude, (as the second of the above mentioned tasks) an investigation into the proportions of such a multiplicity, and into the conditions which are sufficient for determining these.

These dimensional relations can only be investigated in abstract concepts of quantity and represented in context by formulae; under certain conditions, however, they can be reduced to ratios which, taken individually, are capable of geometric representation, and thus it becomes possible to express the results of this calculation geometrically. In this way, to reach solid ground, abstract investigations into formulae are unavoidable, the results of which can be represented in gemometric form. For both are contained in the famous treatise of Privy Councillor Gauss on curved surfaces.

§ 1.

Determinations of measure require for quantity to be independent of position, which may happen in more than one way; the first assumption that presents itself, which I want to pursue here, is that length of these lines is independent of place, thus every line is measurable by every line. If the determination of position is reduced to the determination of quantity, thus the position of a point in the n-fold extended multiplicity is expressed by n variable quantities x₁, x₂, x₃,..., x_n, so the determination of a line will come to giving the quantities x as a function of variable. The task then is to establish a mathematical expression for the length of these lines, for which purpose the quantities x must be considered as expressible in terms of units. I shall treat this task only through certain restrictions, and I shall confine myself in the first place to lines in which the relations between the quantities dx--the related axes--of the quantities x change continuously. Then one can think of the lines divided into elements, within which the ratios of the quantities dx may be regarded as constant, and the task then comes to establishing, for each point, a general expression for the linear element ds derived from it, an expression which will contain the quantities x and dx. I now assume secondly that the length of hte linear element, apart from second order quantities, remains unchanged if all of its points undergo the same infinitesimal change of position which at the same time implies that if all quantities dx grow in the same ratio, the linear element in the same ratio, the linear element also changes with respect to this ratio. With these assumptions, the linear element can be any homogeneous function of the first degree of the quantities dx, which remains unchanged if we change the sign of all the quantities dx, and in which the arbitrary constants are continuous functions of the quantities x. To find the simplest cases, I first seek out an expression for the (n-1) times extended multiplicities which are at every point equally far from the initial point of the linear element (i.e. I am looking for a continuous function of the position whose values distinguishes them from each other). By going outward from the initial point, this must either increase or decrease in all directions; I will assume that it increases on all sides and therefore has a minimum at that initial point. Then it is the case that if their first and second differential quotients are finite, the differential of the first order must vanish and the second order differential must never become negative; I assume that it will always remain positive. This differential expression of the second order remains constant when ds remains constant and it grows in a quadratic proportion if the quantities dx (and thus also ds) increase in the same proportion. It must therefore be a constant multiplied with ds^2, and it follows that ds is the square root of an always positive integral homogeneous function of the second order of the quantities dx, in which the coefficients are continuous functions of the variables x. For space, when the position of points is expressed by right-angled coordinates, is ds = 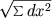, contained in this simplest case. The next simplest case would probably be the multiplicities in which the linear element can be expressed by the fourth root of a differential expression of the fourth degree. The investigation of this more general class would not require any other principles, but it would be rather time consuming and throw little new light on the doctrine of space, especially since the results cannot be expressed geometrically. I will therefore restrict myself to the multiplicities, where the linear element is given by the square root of a differential expression of the second order. One can transform such an expression into another similar one, if we substitute for n independent variables functions of n new independent variables. In this way, however, we cannot transform any expression into another, because the expression contains (n*(n+1))/2 coefficients which are arbitrary functions of the independent variables by introducing new variables, however, one will satisfy only n relations and thus only n of the coefficients given quantities n can be made equal. Then the remaining (n*(n+1))/2 are determined by the nature of the multiplicity to be represented, and for the determination of their dimensional ratios therefore (n*(n+1))/2 functions of location are necessary. The multiplicities in which, (as in the plane and in space) the linear element may be reduced to the form 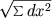, are therefore only a particular case of the multiplicities to be investigated here; they deserve a special name, and so I want to describe these multiplicities, in which the square of the linear element is reduced to the sum of the quadratic of independent differentials, as being flat. In order to now see the essential differences of all multiplicities that can be represented in the assumed form, it is necessary to remove the difficulties arising from the mode of representation by choosing the variable quantities in accordance with a certain principle.

§ 2.

To this end, imagine a given point, and from that given point, constructing a system of shortest lines going out from it, the position of an indeterminate point can be determined by the initial direction of the geodesic line in which it lies, and by its distance from the starting point and can therefore be determined by the ratios dx₀ of the quantities dx in this geodesic, and of the length s of this line. Now let us substitute instead of dx*₀ linear functions, the dα formed from then, so that the initial value of the square of the linear element becomes equal to the sum of the squares of these expressions, so that the independent variables are: the quantity s and the ratio of the quantities dα, and finally, instead of dα, set them to proportional quantities x₁, x₂, ..., x_n, so that the sum of their squares = s^2. When we introduce these quantities, the square of the linear element is \sum dx^2 for infinitesimally small values of x, but the term of the next order in it is equal to a homogeneous function of the second order of (n*(n+1))/2 quantities (x₁ dx₂ − x₂ dx₁ ), (x₁ dx₃ − x₃ dx₁ ), ..., an infinitesimal therefore of the fourth order, so that we get a finite quantity by dividing it by the square of the infinitesimal triangle, whose vertices are (0, 0, 0, ...), (x₁, x₂, x₃, ...), (dx₁, dx₂, dx₃, ...). This quantity retains the same value, so long as x and the dx are included in the same binary linear form, or so long as both geodesics from 0 to x and 0 to dx remain in the same surface-element, and therefore depends only on location and direction. It is obviously equal to zero when the multiplicity is represented as flat (i.e. the square of the linear element is reducible to 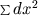, and may therefore be defined as the measure of the deviation of the multiplicity from the flatness at the given point in the given surface-direction. Multiplied by -3/4 it is equal to the quantity, which Lord Privy Councillor Gauss has called the total curvature of a surface. For the determination of the proportions of an n-fold extened multiplicity capable of representation in the form (n*(n+1))/2 functions of location were found necessary; so if the curvature at each point in (n*(n+1))/2 surface-directions is given, the proportions of the multiplicity can be determined from it, provided that there are no identical relations among these values, which in fact, to speak generally, is not the case. The proportions of these multiplicities where the linear element is given by the square root of a quadratic differential may be express in a way that is fully independent of the chosen independent variables. A very similar way can be found for the multiplicities in which the linear element can be represented by a less simple expression, (e.g. the fourth root of a quartic differential). In this case the linear element, generally speaking, is no longer reducible to the form of the square root of a sum of squares, and therefore the deviation from flatness in the squared linear element is an infinitesimal of the second order, while in those multiplicities it was an infinitesimal of the fourth order. This peculiarity of the latter multiplicities may consequently be called flatness of the smallest parts. The most important property of these multiplicities for our present purpose, for which alone they are investigated here, is that the relations of the doubly extended multiplicities are geometrically represented by surfaces and those who have greater number of extension can be traced back to the surfaces contained in them, which now still requires a short discussion.

§ 3.

In the conception of surfaces, together with the inner proportions in which only the length of lines on the surfaces are considered, there is always mixed in the position of point lying outside the surface. But we can abstract from the external relations by making any changes that would leave the lengths of the lines in them unchanged (i.e. if we think of htem as bent in any way without stretching and treate all surfaces related to each other in this way as being of the same kind). Thus, for example, any cylindric or conic surface are equal to a plane because they can be formed out of it by merely bending the plane, whereby the internal proportions and all the theorems about them--i.e. the whole of planimetry--remain valid. On the other hand, they are considered to be essentially different from the sphere, which cannot be transformed into a plane without stretching. After the previous investigation, in each point the internal proportions of a twofold extended quantity in which the linear element can be defined by the square root of a quadratic differential, which is the case with surfaces, are characterized by the total curvature. Now this quantity can be visualized in the case of surfaces as the product of the two curvatures of the surface, or its product can be divided into a geodesic by a geodesic triangle that is equal to half the excess of its angular sum over two rectangles in parts of the radius. The first definition would require the theorem that the product of the two radii of the the curvature is unchanged by merely bending it, the second, that in the same point the area of a small triangle is proportional to its spherical excess. In order to find the curvature of an n folded multiplicity at a given point and with a given direction of the plane through it, one has to assume that a geodesic starting from a point is already entirely determined when the initial direction is given. From this, a certain surface will be obtained if all the lines starting from the given point and lying along the given surface-direction; this surface has at the given point a definite curvature at the given point, which is simultaneously the curavture of the n-fold extended multiplicity at the given point in the given surface-direction.

§ 4.

Now before applying this to space, some considerations about plane multiplicities in general are necessary, (i.e. concerning those in which the square of the linear element is representable by a square sum of complete differentials).

In a plane multiplicity extended n times, the curvature is zero at every point in every direction. However, according to the previous investigation it is sufficient for determining the ratios to know that at every point the curvature is zero in ½ n (n - 1) surface directions. multiplicities whose curvature is constantly zero may be treated as a special case of multiplicities whose curavture is constant everywhere. The shared character of these multiplicities, whose curvature is constant, can also be expressed in such a way, that the figures in them can be moved without stretching. For obviously the figures in them could not be arbitrarily movable and rotatable, if the measure of curvature were not the same at every point in all directions. On the other hand, the ratios of the multiplicity are completely determined by the curvature; therefore they are exactly the same in all directions at point as at another, and consequently the same constructions can be formed out of it, and consequently in multiplicities with a constant curvature, the figures can be given any position. The ratios of these multiplicities depend only on the value of the curvature and with respect to the analytic representation it may be noted that if this value is denoted by α, the expression for the linear element can be written as .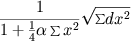

§ 5.

To explain this geometrically, consider the theory of surfaces of constant curvature. It is easy to see that surface whose curvature is positive may move along a sphere, whose radius is equal to 1 divided by the root of the curvature. But in order to see the entire multiplicity nature of these surfaces, let one of them have the shape of a sphere and the others the shape of surfaces of revolution, which meet at the equator. The surfaces with a larger curvature than this sphere will then touch the sphere from the inside and assume the shape of the outer part of the surface of a ring facing away from the axis. They would be located in zones of spheres with a smaller radius, but more than once they would reach around. The surfaces with smaller positive curvature can be obtained so that surface regions may also be moved arbitrarily along the surface without bending them, namely they can be formed into sphere surfaces; but not those with negative curvature. Besides this, the surface with zero curvature is also independent of the direction from the location, which is not the case for other surfaces.

III. Application to Space

§ 1.

After these investigations into determining the ratios of an n-fold extended quantity, we now have the sufficient and necessary conditions to determine the metric ratios of space, if we assume the independence of line length from position and representation of the linear element as the square root of a quadratic differential, that is to say, flatness in the smallest parts.

Firstly, they may be expressed in such a way that the curvature at each point is zero in three directions along the surface, and therefore the metric ratios of space are determined if the sum of the angles of a triangle is always equal to two right angles.

Secondly, if like Euclid, one does not only assume the existence of the lines but also of the bodies, it follows, that the curvature is constant everywhere and then the sum of the angles is determined in all triangles when it is known in one of them.

Third, instead of assuming the length of the lines is independent of position and direction, we could also assume an independence of their length and direction from the location. According to this view, the changes or differences of position are complex quantities expressible in three independent units.

§ 2.

Over the course of the previous reflections, we first separated extension and partition from dimensional relations and found that different dimensional ratios are conceivable for the same proportions; we then investigated the system of simpler dimensions by which the proportions of space are completely determined and from which all these propositions are a necessary consequence. It now remains to see how, and to what extent these conditions are demonstrated by experience. In this respect, there is an essential difference between mere extension and proportion, insofar as in the former, where possible cases form a discrete multiplicity, the assertions of experience are never completely certain, though not inaccurate. In the latter, where the possible cases form a continuous multiplicity, any determination from experience always remains inaccurate; even if the probability is so great that it is nearly exact. This becomes important when extending empirical determinations beyond the limits of observation into the infinitely large and infinitesimally small. The latter can obviously become more and more inaccurate beyond the limits of observation, but the former cannot become more and more inaccurate.

In extending spatial construction to the infinitely large, we must distinguish between unbounded and infinite in extent. The former belongs to relations of extension, teh latter to relations of measurement. It is a prerequisite fact that space is an unbounded, threefold extended multiplicity which is applied to every conception of the external world, according to which the area of real perception is completed at every instant and the possible positions of a sought object are constructed, and which is constantly confirmed by these applications. The boundlessness of space has a greater empirical certainty than any external experience. However it does not at all follow from this that it is infinite in extent. Rather, assuming bodies are independent of space and by ascribing a constant curvature to it, space would necessarily be finite as soon as the curvature has an even small positive value. If we extended the initial directions lying along the surface element to the geodesic lines, we would obtain an unlimited surface with a constant positive measure of curvature (i.e. a surface which in a flat multiplicity of three dimensions would take the form of a sphere and consequently be finite).

§ 3.

Questions about the infinitely large are useless questions when it comes to the interpretation of nature. But this is not the case for questions concerning the infinitesimal. Our knowledge of causal relations essentially depends on the exactness with which we trace phenomena into the infinitesimal. The scientific advances of the last centuries in the knowledge of mechanical nature are almost solely due to the precision of this construction which was made possible by the invention of the analysis of the infinite and the simple concepts discovered by Archimedes, Galileo, and Newton which today's physics makes use of and is made possible by. In the science where the simple concepts for such constructions are still missing, in order to recognize the causal connection, one must pursue the phenomena into the spatially small, as far as the microscope allows. Questions about spatial proportions in what is unmeasurable are therefore not useless.

If one presupposes bodies exist independent of space, the curvature is constant everywhere, and it then follows from astronomical measurements that it cannot be different from zero or in any case, its reciprocal value must be an surface against which the area in reach of our telescopes would have to disappear. But if we do not presuppose the independence of bodies from space, then one cannot deduce proportions on the infinitesimal scale from the infinitely large scale. At each the point the curvature in three directions can have any arbitrary value, if only the whole curvature of each measurable part of space is not noticeably different from zero. Even more complicated relations may occur if the assumed representation of a linear element by the square of a linear element by the square root of a quadratic expression does not occur. Now hoever the empirical concepts in which spatial measurements are based--the concept of the solid body and of the light ray--lose their validity in the infinitesimal. Therefore it is very well conceivable that the proportions of space in the infinitesimal are not in accordance with the presuppositions of geometry, and we should assume this if we can therefore explain phenomena in a simpler way.

The question about the validity of geometry's presuppositions with regard to the infintesimal is bound up with the question of the ground of measuring spatial relations. In this question, which may still be counted as part of the doctrine of space, the above observation is applied, that in the case of a discrete multiplicity, this principle is already contained in the cocnept of the multiplicity, but in the case of a continuous multiplicity it must be grounded somewhere else. Therefore, the reality undergirding space must form a discrete multiplicity, or we must seek out the ground of its metric relations outside it, in the binding forces which act on it. The resolution of these questions can only be discovered by starting from the previous conception of the phenonema, which has been proven by experience and for which Newton laid the foundation, and by gradually reworking this conception through facts which it cannot explain. Research starting from general concepts, such as the investigation here, can only serve to ensure that this work is not hindered by the limitations of concepts and that progress in recognizing the connections of things cannot be hindered by traditional prejudices.

This leads into another science, the field of physics, which the nature of the current investigation does not permit us to enter.